고정 헤더 영역
상세 컨텐츠
본문
지난 시간 [수학과 함께하는 AI기초_01(이미지데이터처리)] https://kimilguk.tistory.com/894 에 이어서
온라인강좌) EBS 이솦: https://www.ebssw.kr/lrnng/alctcr/alctcrDetailView.do?alctcrSn=56134
- 강좌명 : 수학과 함께하는 AI기초 #1 - 데이터의 표현과 가공
- 14개 챕터(장), 31개 강의로 이루어 져 있고, 지금 9-1 ~ 12-1장(챕터) 사이를 하고 있습니다.
오늘은 소리 데이터를 불러와서 처리하는 과정을 알아 보도록 하겠습니다.
우선 공개된 윈도우 종료 음악을 불러와서 샘플주파수(sin그래프)와 재생시간 및 numpy 배열데이터를 확인하고,
매트플로트 화면에 그래프로 표시하는 결과부터 확인 해 보겠습니다.(아래)

- 위 왼쪽 하단 CMD창에 필요한 scipy(42.2메가)와 sounddrive(약500KB) 라이브러리 2개를 설치하는 화면 입니다.(참고로, 삭제는 pip uninstall 라이브러리명)
- 위 소스에 사용된 윈도우 종료 사운드(wav)파일은 아래와 같습니다.(아래)
- 위 실행 소스는 아래와 같습니다.(아래)
import numpy as np # 행렬 데이터 처리 라이브러리
import matplotlib.pyplot as plt
import scipy.io.wavfile # wav파일 처리 라이브러리
import sounddevice as sd # wav파일 재생 라이브러리
# 단위 주파수(samplerate)와 전체 소리데어터 구하기(아래)
v_samplerate, v_data = scipy.io.wavfile.read("windows_end.wav")
times = np.arange(len(v_data))/float(v_samplerate) # x축 배열 갯수=시간정보 구하기
print('sampling rate: ', v_samplerate) # 샘플링 주파수(sign그래프의 주기) 확인
print('time : ', times[-1]) # x출 소리의 제일 마지막 재생시간 확인
print('vData : ', v_data[5000:5100]) # 5000번째 주파수의 데이터확인
sd.play(v_data, v_samplerate) # wave 파일재생
# 소리 매트플로트 화면에 그래프로 출력
plt.plot(times, v_data)
plt.xlim(times[0], times[-1]) # 시간x축의 영역을 play시간으로 limt제한
plt.xlabel('time(s)')
plt.ylabel('amplitude') # 진동폭=소리의 비트처리확인 8비트~
plt.show()
Ps. 고주파와 저주파의 차이(아래)
- 반복수(주기)가 고주파가 > 저주파 보다 빠르다=많다.(아래그래프참조). 또한, 대체로 저주파는 상하로 큰 진폭을 가지고 있다.

- 일반적으로 사람에게 고주파는 가늘고 날카로운 소리, 저주파는 굵고 부드러운 소리로 들립니다.
## 이번 학습의 핵심은 삼각함수의 θ라디안(x)변수 변화에 따른 그래프 모양을 아래 PS.수학개념으로 알게 된다는 것이 핵심이다.
- 사인(sin)함수의 그래프는 반지름이 1인 원에서 θ라디안(x)의 변화에 따라 삼각형의 높이(y)의 크기가 변한다.(*핵심이론)
∠θ 0도부터 시작하는 sinθ(높이/빗변)는 좌표가 (0,0)부터 시작하고, y는 1을 넘지 않고 반복하는 모양(주기=2π라디안 )를 갖는다.(아래)

- 코사인(cos)함수의 그래프는 반지름이 1인 원에서 θ라디안(x)의 변화에 따라 삼각형의 밑변(y)의 크기가 변한다.
∠θ 0도부터 시작하는 cosθ(밑변/빗면)는 좌표가 (0,1)부터 시작하고, y는 1을 넘지 않고 반복하는 모양(주기=2π라디안 )를 갖는다.(아래)

- 탄젠트(tan)함수의 그래프는 반지름이 1인 원에서 θ라디안(x)의 변화에 따라 삼각형의 높이(y)의 크기가 변한다.
∠θ 0도부터 시작하는 tanθ(높이/밑변)는 좌표가 (0,0)부터 시작하고, y는 무한대로 향하고 반복하는 모양(주기=π라디안 )를 갖는다.(아래)

- 위 sin함수의 그래프등은 전자분야 오실로스코프 주파수 측정에도 자주 보이는 모양이라서 꼭 알고 있어야 합니다.
Ps. 위 그래프를 이해하기 위해서 필요한 수학 개념으로 기준각(θ,세타)사인(sin),코사인(cos),탄젠트(tan) 함수와 그래프를 확인해 보겠습니다.(아래)
- 사용되는 그래스 문자: θ 세타, π 파이(원주율,원의 지름에 대한 둘레의 비율을 나타내는 수학 상수=3.141592...)
##호도(radian)법이란?: 주파수 주기 그래프에서 사용되는 단위를 위해 "호의 길이를 각도로 나타내는 방법"으로 그 단위는 라디안 rad(radian)로 한다.
- 반지름과 호의 길이가 같을 때의 내각을 1라디안이라고 한다(아래)
1라디안은 반지름이 1인 원에서 아래와 같은 개념으로 1라디안을 구할 수 있다.
∠ 360도 : 2π1(반지름) = ∠ θ각도 : 1(반지름) ----> 180도/π = 1라디안 -----> π라디안=180도

- 그래서 앞으로 π라디안(3.14...rad) = 180도를 기준으로 계산한다.(아래)
암산할때, π/6 라디안을> θ각도로 변환하는 계산은 180을 기준으로 6*30=180이 되므로 30도이다.
암산할때, 반대로 60도를> π라디안으로 변환하는 계산은 180을 기준으로 60*3=180이 되므로 π/ 3라디안이다.
##삼각비란?: 밑변과 높이가 각각 1인 직각 삼각형의 기준각의 라디안 값을 기준으로 세변은 정해진 비율을 가진다(아래)

참고로, sin은 필기체의 사인모양으로 이미지메이킹해서 빗변 분의 높이를 기억한다.(아래)

- 삼각함수로 계산시 아래 표를 띄워놓고 계산한다.(아래)

- 또는 위 표를 외우지 말고, 아래 도형을 그려놓고, 삼각함수 계산시 사용하면 된다.(아래)

- 예제 풀기(힌트, 아래 문제는 π/6 표의 삼각비를 사용하면 구할 수 있다.)

##삼각함수란? 좌표에서 θ라디안(각도)값의 변화에 따른x, y값의 변화 즉, 좌표를 구하는 것이라고 할 수 있다.(아래)

- 위 삼각함수 개념을 사용하여 문제를 풀어보자(아래)

- 위 기준각은 π/3 표를 이용하여 삼각함수 θ라디안(각도) 값의 변화에 따른 x, y(좌표)값을 구하면 된다.
sin π/3(반지름이 1이라서) = -√3/2 (y좌표)
cos π/3(반지름이 1이라서) = -1/2(x좌표)
tan π/3 = √3
## 12-1 장(챕터)의 소리파일 생성하기-위 에서 알아본 삼각함수의 그래프에 대한 수학 지식을 기반으로...(아래)
import numpy as np
import matplotlib.pyplot as plt
from scipy.io.wavfile import write
import os
# sampling rate 변수생성(아래)
Fs = 1000.0 # 1초에 1000번의 주기를 갖는다.
tlen = 1 # 1초 간 실행시간
Ts = 1/Fs
t = np.arange(0, tlen, Ts) # 0과 1사이를 1000개로 분할해서 진행시간을 저장
# sin사인 함수를 사용하여 소리 데이터 만들기(아래)
sin_freq = 100 # sin 곡선의 주기는 아래 (y=360도인 2pi*주기) = 여기서는 100번-고주파/저부파 결정
# t배열100개의 각항목에 sin주기10개를 라디안 단위2pi로 변환한 src배열준비(아래)
src = 2*np.pi*sin_freq*t # 즉, 소리의 세로(y축) 배열의 크기가 생성된다.
signal = np.sin(src) # sin 라디안값의 y좌표(궤적)을 데이터로 생성
# 참고로 위 sin함수 값에 10을 곱하면, 진폭(y 의 크기)가 1에서 10으로 커진다.
#signal = 100*np.sin(src) # 주기는 그대로이지만, 소리의 크기(음량 결정)가 커진다.
# 위 sin라디안 데이터를 플로트에 표시(아래)
x_range = 1000 # sin라디안인 x 값을 1000개 까지만 보여주기
plt.plot(t[0:x_range], signal[0:x_range], color = 'blue')
plt.show()
# Fast Fourer Transform = fft 푸리에 변환,주어진 파형에서 주파수를 표시(아래)
freq = np.fft.fftfreq(len(t), Ts)
# 위 기존 소리의 세로배열(사인라디안값)에서 주파스크기를 가져오는 함수 사용(아래)
signal_f = np.fft.fft(signal) # 결과값은 허수가 포함된 복소수 이다.
# 좌표의 가로축이 시간에서 주파수로 변경된 것을 확인(아래)
plt.plot(freq[0:x_range], 20*np.log10(np.abs(signal_f[0:x_range])),color='blue')
plt.show()
# 허수의 절대값이 너무 크기 때문에 아래 처럼 y축의 값을 조정한다.(양수쪽만 표시)
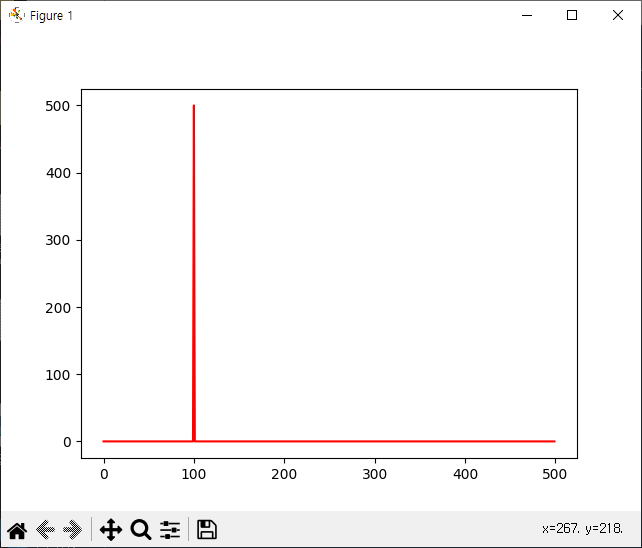
plt.plot(freq[0:x_range//2], (np.abs(signal_f[0:x_range//2])),color='red')
plt.show()
# 위 데이터를 wav로 저장하기(아래)
# 신호/신호의절대값의최고값으로 나눈다.=정규화(0부터 1사이틔 값으로 변환)+계산하기 편리
scaled = np.int16(signal/np.max(np.abs(signal)) * 32767)
write('sin_signal.wav', 1000, scaled) # 주기는 코드 상단의 Fs와 동일하게- 위 소스에서 정규화란? [개별값들/전체개별값 중 최대값 = 0~1사이로 값이 변환]을 아래식과 같이 예를 들면, 어떤 계산식이 더 간단할 것인가? 판단할 수 있다.
비교 계산식: 1,000,000/10,000,000 = 1/10 (즉, 1/10 으로 변경해서 계산하는 식이 더 간단하다.)
- 위 소스에서 1초당 주기횟수인 주파수가 100이라는 것을 사인 함수의 그래프로 확인할 수 있다.(아래)

- 위 소리의 주파수 사인 함수의 그래프에서 푸리에 함수를 이용하여 아래 주파수 그래프로 변경한다.(아래)

- 위 푸리에 함수 그래프를 보기 쉽게 표시한 기능은 위 소스의 제일 하단에 plt.show()함수에서 확인한다.(아래)
'파이썬·장고·루비·알고리즘' 카테고리의 다른 글
| 수학과 함께하는 AI기초_03(소리데이터합성) (1) | 2024.12.17 |
|---|---|
| 수학과 함께하는 AI기초_01(이미지데이터처리) (3) | 2024.12.09 |
| 파이썬으로 웹 스크레핑과 반응형 대시보드 앱 만들기(강의용) (0) | 2024.05.15 |
| 파이썬으로 웹 스크레핑과 반응형 대시보드 앱 만들기 (1) | 2023.03.13 |
| 장고마무리_어깨힘 풀고 파이썬 (0) | 2019.06.01 |






댓글 영역